一道钓鱼题引发的“惨案”

例： x+y+z=1x+y+z=1

证明 xy+yz+xz−xyz≤827xy+yz+xz-xyz\le\frac{8}{27}

证： 先齐次化等价于

(x+y+z)(xy+yz+xz)−xyz≤827(x+y+z)3(x+y+z)(xy+yz+xz)-xyz\le\frac{8}{27}(x+y+z)^3

LHS=(x+y)(x+z)(y+z)≤(2a+2b+2c3)3=RHSLHS=(x+y)(x+z)(y+z)\le(\frac{2a+2b+2c}{3})^3=RHS 证毕

已经学习过例题，那我们证一个“形式相似”的习题

习题：满足条件x+y+z=1x+y+z=1

设 x,y,zx,y,z 构成为最小角正切值大于等于 162−137\frac{\sqrt{16\sqrt{2}-13}}{7} 的三角形的三边。

证明 47xy+47yz+47xz−(542+45)xyz≤378−5422747xy+47yz+47xz-(54\sqrt{2}+45)xyz\le\frac{378-54\sqrt{2}}{27}

第一次做这道题是一年前，严格来说这不是一道钓鱼题，因为它看上去就很难

但当年比较头铁，硬是被钓到了，虽然经历了三个小时的艰苦奋战后终于做出来了

但我记得那天晚上的梦都带着根号。

证明:

因为上式为轮换对称式，所以不妨设 x≥y≥zx\ge y\ge z , zz 为最小边对的角,设最小角为 α\alpha ,所以有:

tanα≥162−137=(362−45)+(32−202)81−32=(42−5)(9+42)(9−42)(9+42)=42−59−42tan\alpha\ge\frac{\sqrt{16\sqrt{2}-13}}{7}=\frac{\sqrt{(36\sqrt{2}-45)+(32-20\sqrt{2})}}{\sqrt{81-32}}=\sqrt{\frac{(4\sqrt{2}-5)(9+4\sqrt{2})}{(9-4\sqrt{2})(9+4\sqrt{2})}}=\sqrt{\frac{4\sqrt{2}-5}{9-4\sqrt{2}}}

tan2α=sin2αcos2α=1−cos2αcos2α≥42−59−42⇒cos2α≤9−424=(22−12)2tan^2\alpha=\frac{sin^2\alpha}{cos^2\alpha}=\frac{1-cos^2\alpha}{cos^2\alpha}\ge\frac{4\sqrt{2}-5}{9-4\sqrt{2}}\Rightarrow cos^2\alpha\le\frac{9-4\sqrt{2}}{4} =(\frac{2\sqrt{2}-1}{2})^2

因为 α\alpha 为最小角小于 60∘60^\circ ，所以推出

cosα≤22−12cos\alpha\le\frac{2\sqrt{2}-1}{2}\\ (1)(1)

余弦定理 x2+y2−z22xy=cosα≤22−12⇒x2+y2−(22−1)xy≤z2\frac{x^2+y^2-z^2}{2xy}=cos\alpha\le\frac{2\sqrt{2}-1}{2}\Rightarrow x^2+y^2-(2\sqrt{2}-1)xy\le z^2 (2)(2)

由均值不等式有 22+12xy≤22+14x2+22+14y2\frac{2\sqrt{2}+1}{2}xy\le\frac{2\sqrt{2}+1}{4}x^2+\frac{2\sqrt{2}+1}{4}y^2 (3)(3)

将 (1)(1) 代入 (2)(2) z2≥3−224(x+y)2=(2−12)2(x+y)2z^2\ge\frac{3-2\sqrt{2}}{4}(x+y)^2=(\frac{\sqrt{2}-1}{2})^2(x+y)^2 推出

z≥2−12(x+y) z\ge\frac{\sqrt{2}-1}{2}(x+y)\\ (4)(4)

接下来我们回到原不等式的证明

378−54227≥47xy+47yz+47xz−(542+45)xyz\frac{378-54\sqrt{2}}{27}\ge47xy+47yz+47xz-(54\sqrt{2}+45)xyz

⇔423−45−5431269≥xy+yz+xz−542+4547xyz\Leftrightarrow \frac{423-45-54\sqrt{3}}{1269}\ge xy+yz+xz-\frac{54\sqrt{2}+45}{47}xyz

⇔(4231269−xy+yz+xz(x+y+z)2)≥542+4547(127−xyz(x+y+z)3)\Leftrightarrow(\frac{423}{1269}-\frac{xy+yz+xz}{(x+y+z)^2})\ge\frac{54\sqrt{2}+45}{47}(\frac{1}{27}-\frac{xyz}{(x+y+z)^3})

⇔(13−xy+yz+xz(x+y+z)2)≥542+4547(127−xyz(x+y+z)3)\Leftrightarrow(\frac{1}{3}-\frac{xy+yz+xz}{(x+y+z)^2})\ge\frac{54\sqrt{2}+45}{47}(\frac{1}{27}-\frac{xyz}{(x+y+z)^3})

LHS=x2+y2+z2−xy−yz−xz3(x+y+z)2=(x−y)2+(y−z)2+(z−x)26(x+y+z)2LHS=\frac{x^2+y^2+z^2-xy-yz-xz}{3(x+y+z)^2}=\frac{(x-y)^2+(y-z)^2+(z-x)^2}{6(x+y+z)^2}

RHS=542+4547⋅x3+y3+z3+3x2y+3xy2+3y2z+3yz2+3x2z+3xz2−21xyz27(x+y+z)3RHS=\frac{54\sqrt{2}+45}{47}\cdot\frac{x^3+y^3+z^3+3x^2y+3xy^2+3y^2z+3yz^2+3x^2z+3xz^2-21xyz}{27(x+y+z)^3}

=542+4547(x3+y3+z3−3xyz)+3(x2y+xy2+y2z+yz2+x2z+xz2−6xyz)27(x+y+z)3=\frac{54\sqrt{2}+45}{47}\frac{(x^3+y^3+z^3-3xyz)+3(x^2y+xy^2+y^2z+yz^2+x^2z+xz^2-6xyz)}{27(x+y+z)^3}

=542+4547⋅12(x+y+z)((x−y)2+(y−z)2)+(x−z)2)+3(x(y−z)2+y(x−z)2+z(x−y)2)27(x+y+z)3=\frac{54\sqrt{2}+45}{47}\cdot\frac{\frac{1}{2}(x+y+z)((x-y)^2+(y-z)^2)+(x-z)^2)+3(x(y-z)^2+y(x-z)^2+z(x-y)^2)}{27(x+y+z)^3}

所以原式等价于

9(x+y+z)((x−y)2+(y−z)2+(x−z)2)9(x+y+z)((x-y)^2+(y-z)^2+(x-z)^2)

≥542+4547((x+y+7z)(x−y)2+(x+7y+z)(x−z)2+(7x+y+z)(y−z)2)\ge\frac{54\sqrt{2}+45}{47}((x+y+7z)(x-y)^2+(x+7y+z)(x-z)^2+(7x+y+z)(y-z)^2)

⇔∑cyc((9−542+4547)x+(9−542+4547)y+(9−7⋅542+4547)z)(x−y)2≥0\Leftrightarrow\sum_{cyc}((9-\frac{54\sqrt{2}+45}{47})x+(9-\frac{54\sqrt{2}+45}{47})y+(9-7\cdot\frac{54\sqrt{2}+45}{47})z)(x-y)^2\ge0

⇔∑cyc(378−54247x+378−54247y−3782−10847z)(x−y)2≥0\Leftrightarrow\sum_{cyc}(\frac{378-54\sqrt{2}}{47}x+\frac{378-54\sqrt{2}}{47}y-\frac{378\sqrt{2}-108}{47}z)(x-y)^2\ge0

于是我们只需证明:

⇔(x+y−2z)(x−y)2+(x+y−2z)(x−y)2+(x+y−2z)(x−y)2≥0\Leftrightarrow(x+y-\sqrt{2}z)(x-y)^2+(x+y-\sqrt{2}z)(x-y)^2+(x+y-\sqrt{2}z)(x-y)^2\ge0

令 Sz=x+y−2zS_z=x+y-\sqrt{2}z Sy=x+z−2yS_y=x+z-\sqrt{2}y Sx=y+z−2xS_x=y+z-\sqrt{2}x

⇔Sx(y−z)2+Sy(x−z)2+Sz(x−y)2≥0\Leftrightarrow S_x(y-z)^2+S_y(x-z)^2+S_z(x-y)^2\ge0

Sx(y−z)2+Sy(x−z)2+Sz(x−y)2 S_x(y-z)^2+S_y(x-z)^2+S_z(x-y)^2

=Sy(x−y+y−z)2+Sx(y−z)2+Sz(x−y)2=S_y(x-y+y-z)^2+ S_x(y-z)^2+S_z(x-y)^2

=(Sx+Sy)(y−z)2+(Sy+Sz)(x−y)2+2(x−y)(y−z)Sy=(S_x+S_y)(y-z)^2+(S_y+S_z)(x-y)^2+2(x-y)(y-z)S_y

所以只需证 Sx+Sy≥0S_x+S_y\ge0, Sy+Sz≥0S_y+S_z\ge0, Sy≥0S_y\ge0 即可

Sx+Sy=2z−(2−1)(x+y)S_x+S_y=2z-(\sqrt{2}-1)(x+y) 由 (4)(4) 知上式成立

Sy+Sz=S_y+S_z= 2x−(2−1)(y+z)≥02x-(\sqrt{2}-1)(y+z)\ge0

2Sy≥Sx+Sy≥0⇔y≥z2S_y\ge S_x+S_y\ge0\Leftrightarrow y\ge z 上式因为 x≥y≥zx\ge y\ge z 所以显然成立

所以原不等式得证，当且仅当 x=y=zx=y=z 与x=y=(2+1)zx=y=(\sqrt{2}+1)z 及其轮换时等号成立

昨天在整理草稿的时候，又重新将这道题做了一遍，发现这道题实际来自一个推广。

先考虑例的简单情况的推广

x+y+z=1x+y+z=1 时 (xy+yz+xz−txyz)max(xy+yz+xz-txyz)_{max}

当 x=y=z=13x=y=z=\frac{1}{3} 有 xy+yz+xz−txyz=9−t27xy+yz+xz-txyz=\frac{9-t}{27}

当 x=y=12x=y=\frac{1}{2}, z=0z=0 有 xy+yz+xz−txyz=14xy+yz+xz-txyz=\frac{1}{4}

所以猜测有推广一: xy+yz+xz−txyz≤max{9−t27,14}xy+yz+xz-txyz\le max\{\frac{9-t}{27},\frac{1}{4}\}

更直观的写有

xy+yz+xz−txyz≤9−t27xy+yz+xz-txyz\le\frac{9-t}{27} (0≤t≤94)(0\le t\le\frac{9}{4})

xy+yz+xz−txyz≤14xy+yz+xz-txyz\le\frac{1}{4} (t≥94)(t\ge\frac{9}{4})

证:下面将要证式分为 t∈[0,94]t\in[0,\frac{9}{4}] , t∈[94,3]t\in[\frac{9}{4},3] , t∈[3,+∞]t\in[3,+\infty] 三种情况证明

因为上式为轮换对称式，所以不失一般性，我们设 x≥y≥zx\ge y\ge z

定义 f(x,y,z)=xy+yz+xz−txyzf(x,y,z)=xy+yz+xz-txyz

引理: t∈[0,3]t\in[0,3] 时有 f(x,y,z)≤f(x+y2,x+y2,z)f(x,y,z)\le f(\frac{x+y}{2},\frac{x+y}{2},z)

t∈[3,+∞]t\in[3,+\infty] 时有 f(x,y,z)≤f(x,y+z,0)f(x,y,z)\le f(x,y+z,0)

1. x≥y≥z⇒3z≤x+y+z=1⇒z≤13⇒zt≤1x\ge y\ge z\Rightarrow3z\le x+y+z=1\Rightarrow z\le\frac{1}{3}\Rightarrow zt\le1 由均值不等式有

f(x,y,z)=z(x+y)+(1−tz)xy≤z(x+y)+(1−tz)(x+y2)2=f(x+y2,x+y2,z)f(x,y,z)=z(x+y)+(1-tz)xy\le z(x+y)+(1-tz)(\frac{x+y}{2})^2=f(\frac{x+y}{2},\frac{x+y}{2},z)

2, x≥y≥z⇒3x≥x+y+z=1⇒x≥13⇒xt≥1x\ge y\ge z\Rightarrow3x\ge x+y+z=1\Rightarrow x\ge\frac{1}{3}\Rightarrow xt\ge1

f(x,y,z)=x(y+z)+(1−xt)yz≤x(y+z)=f(x,y+z,0)f(x,y,z)=x(y+z)+(1-xt)yz\le x(y+z)=f(x,y+z,0)

所以引理得证，回到原题

(1)(1) t∈[0,3]t\in[0,3] 时 令 x+y2=a\frac{x+y}{2}=a (12≥a≥13)(\frac{1}{2}\ge a\ge\frac{1}{3})

f(a)=2(1−2a)a+(1−t+2at)a2=2ta3−(3+t)a2+2af(a)=2(1-2a)a+(1-t+2at)a^2=2ta^3-(3+t)a^2+2a

f′(a)=2(3a2t−(3+t)a+1)=2(3a−1)(ta−1)f(a)=2(3a^2t-(3+t)a+1)=2(3a-1)(ta-1)

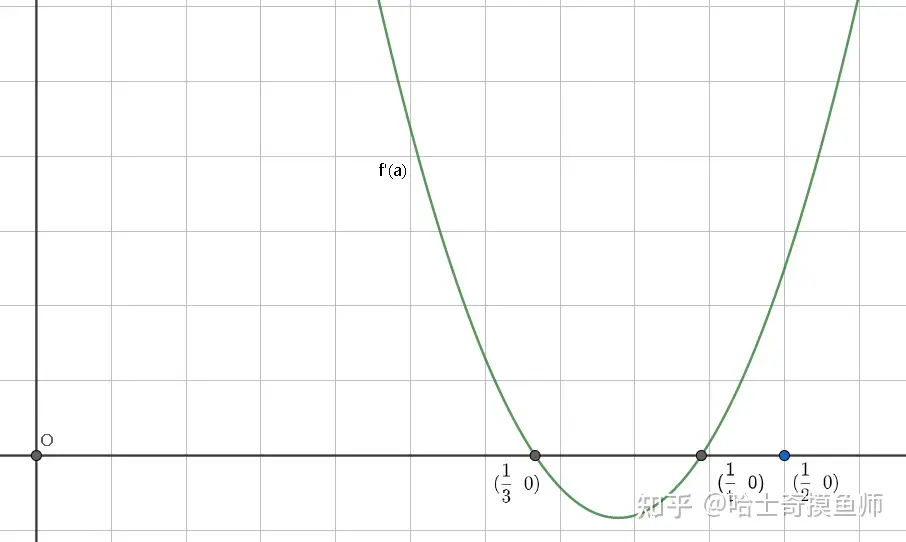
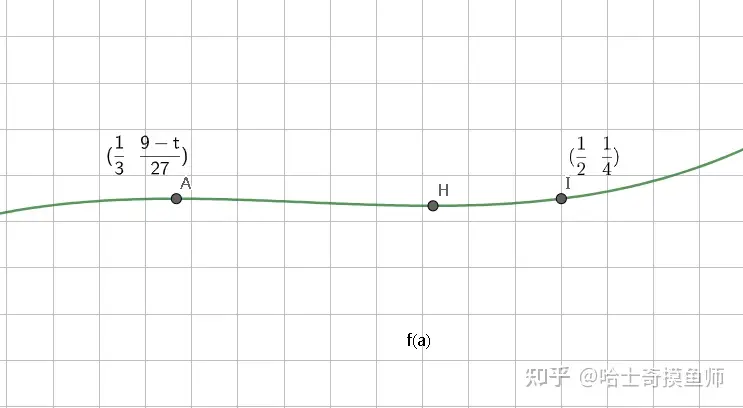
因为 x=13x=\frac{1}{3} , x=12x=\frac{1}{2}为 f(a)f(a)两个极大值点，所以f(a)≤max{14,9−t27}f(a)\le max\{\frac{1}{4},\frac{9-t}{27}\}

即 t∈[0,94]t\in[0,\frac{9}{4}] 时 f(a)≤9−t27f(a)\le\frac{9-t}{27} t∈[94,3]t\in[\frac{9}{4},3] 时 f(a)≤14f(a)\le\frac{1}{4}

(2)(2) t∈[0,3]t\in[0,3] 时 ⇔(x+y)z≤14\Leftrightarrow(x+y)z\le\frac{1}{4}

由均值不等式有 (x+y)z≤(x+y+z2)2=14(x+y)z\le(\frac{x+y+z}{2})^2=\frac{1}{4}

综上所述，推广一得证

对于后面习题的推广，尝试了好多次发现证明与三角函数没什么关系（怀疑三角函数只是单纯为了增大计算量，来坑害年幼无知的孩子）关键条件是 z≥m(x+y)z\ge m(x+y) (m∈[0,12])(m\in[0,\frac{1}{2}])

于是我们从最后一步的S0S（平方分析法）进行入手 (x≥y≥z)(x\ge y\ge z)

Sx+Sy=2z−2m(x+y)≥0S_x+S_y=2z-2m(x+y)\ge0

Sx=z+y−λxS_x=z+y-\lambda x Sy=x+z−λyS_y=x+z-\lambda y ⇒Sx+Sy=2x−(λ−1)(y+z)\Rightarrow S_x+S_y=2x-(\lambda-1)(y+z)

⇒λ=1+2m\Rightarrow\lambda=1+2m

⇒∑cyc(x+y−(2m+1)z)(x−y)2≥0\Rightarrow\sum_{cyc}(x+y-(2m+1)z)(x-y)^2\ge0

⇔∑cycx3+y3−x2y−xy2−(2m+1)(x2z+y2z−2xyz)≥0\Leftrightarrow\sum_{cyc}x^3+y^3-x^2y-xy^2-(2m+1)(x^2z+y^2z-2xyz)\ge0

⇔2∑cycx3−(2m+2)∑cyc(x2y+xy2)+(12m+6)xyz≥0\Leftrightarrow2\sum_{cyc}x^3-(2m+2)\sum_{cyc}(x^2y+xy^2)+(12m+6)xyz\ge0

下面使用待定系数法

a(x+y+z)3+bxyz≥c(x+y+z)(xy+yz+xz)a(x+y+z)^3+bxyz\ge c(x+y+z)(xy+yz+xz)

⇔a∑cycx3+(3a−c)∑cyc(x2y+xy2)+(6a+b−3c)xyz≥0\Leftrightarrow a\sum_{cyc}x^3+(3a-c)\sum_{cyc}(x^2y+xy^2)+(6a+b-3c)xyz\ge0

代入上面的式子得到方程组

{a=23a−c=−2m−26a+b−3c=12m+6\left\{ \begin{array}{**lr**} a=2& \\ 3a-c=-2m-2 & \\ 6a+b-3c=12m+6 & \end{array} \right. ⇒\Rightarrow {a=2b=18m+18c=2m+8\left\{ \begin{array}{**lr**} a=2 & \\ b=18m+18 & \\ c=2m+8 \end{array} \right.

所以有: (x+y+z)3+(9m+9)xyz≥(m+4)(x+y+z)(xy+yz+xz)(x+y+z)^3+(9m+9)xyz\ge(m+4)(x+y+z)(xy+yz+xz)

将条件代入有 xy+yz+xz−9m+9m+4xyz≤1m+4xy+yz+xz-\frac{9m+9}{m+4}xyz\le\frac{1}{m+4}

我们再由 z≥m(x+y)z\ge m(x+y) ⇔\Leftrightarrow z2≥m2(x+y)2z^2\ge m^2(x+y)^2

由均值不等式有 m2(x+y)2≤x2+y2+(4m2−2)xym^2(x+y)^2\le x^2+y^2+(4m^2-2)xy

所以只需满足 z2≥x2+y2+(4m2−2)xyz^2\ge x^2+y^2+(4m^2-2)xy

代入余弦定理有 cosα=x2+y2−z22xy≤cos\alpha=\frac{x^2+y^2-z^2}{2xy}\le 1−2m21-2m^2

tan2α=sin2αcos2α=1−cos2αcos2α≥tan^2\alpha=\frac{sin^2\alpha}{cos^2\alpha}=\frac{1-cos^2\alpha}{cos^2\alpha}\ge 4m2−4m44m4−4m2+1\frac{4m^2-4m^4}{4m^4-4m^2+1}

tanα≥2m2−m41−2m2tan\alpha\ge\frac{2\sqrt{m^2-m^4}}{1-2m^2}

可以用令 x=yx=y 检验得上述不等式为最佳系数

所以我们有推论二： m∈[0,12]m\in[0,\frac{1}{2}]

满足条件x+y+z=1x+y+z=1

设 x,y,zx,y,z 构成为最小角正切值大于等于 2m1−m21−2m2\frac{2m\sqrt{1-m^2}}{1-2m^2} 的三角形的三边。

证明 xy+yz+xz−9m+9m+4xyz≤1m+4xy+yz+xz-\frac{9m+9}{m+4}xyz\le\frac{1}{m+4}

当然还有一个精简版的推论二m∈[0,12]m\in[0,\frac{1}{2}]

满足条件x+y+z=1x+y+z=1 min{x,y,z}≥mm+1min\{x,y,z\}\ge\frac{m}{m+1}

证明 xy+yz+xz−9m+9m+4xyz≤1m+4xy+yz+xz-\frac{9m+9}{m+4}xyz\le\frac{1}{m+4}

原钓鱼题即为 m=2−12m=\frac{\sqrt{2}-1}{2} 的特殊情况

被这道题坑了的我终究是意难平，于是我准备换个“数”拿这道题坑一下别人

1. （521特供，非常温馨的一道题，建议与女朋友一起服用[狗头保命]）

满足条件x+y+z=1x+y+z=1

设 x,y,zx,y,z 构成为最小角正切值大于等于 5211455155591857\frac{521\sqrt{1455155}}{591857} 的三角形的三边。

证明 xy+yz+xz−165155777xyz≤13145777xy+yz+xz-\frac{16515}{5777}xyz\le\frac{1314}{5777} （当m=5211314m=\frac{521}{1314}时成立）

2.(确信，这是一道高考导数题，可以用来与老师一起讨论问题 [狗头保命] )

满足条件x+y+z=1x+y+z=1 ,min{x,y,z}≥eeee+31min\{x,y,z\}\ge\frac{e^e}{e^e+31}

证明 xy+yz+xz−9ee+279ee+124xyz≤31ee+124xy+yz+xz-\frac{9e^e+279}{e^e+124}xyz\le\frac{31}{e^e+124}（当 m=ee31m=\frac{e^e}{31} 时成立）

3.(高考三角函数题,很简单,可以给新高一的小朋友做[狗头保命])

满足条件x+y+z=1x+y+z=1

设 x,y,zx,y,z 构成为最小角大于等于 54∘54^\circ 的三角形的三边。

证明 xy+yz+xz−9sin27∘+9sin27∘+4xyz≤1sin27∘+4xy+yz+xz-\frac{9sin27^\circ+9}{sin27^\circ+4}xyz\le\frac{1}{sin27^\circ+4} （当m=sin27∘m=sin27^\circ时成立）